What is the Real Meaning of Computational Physics

What Truly the Computational Physics is

By: IGA Widagda

June 26, 2020

       Based on the tradition, physics it is divided into two categories: theoretical physics and experimental physics. Theoretical physics is concerned with modeling while experimental physics is related to testing of the model. In the 1980's computer equipment experienced a very rapid development both in terms of hardware and software that gave rise to a new field of study in physics. This new field deals with the research of physics systems with the assistance of computer power. This new field is known as computational physics. There are still debate on opinion about the status of computation in methods related to physics. Occasionally, Computational physics is considered more similar to theoretical one. Other people consider simulation by using computer resembles computer experiments. But some others still consider it is a mediator between theoretical physics and experimental physics. Therefore, Computational physics is a method that supports both theory and experiment (Figure 1).

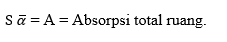
                                           Figure 1 Relationship of Physics: Computational, theoretical and experimental

       Computational physics is a discipline dealing with numerical analysis and its implementation to find the solution of problems in the area of physics associated with quantitative physics theories that have existed earlier. The numerical method is a sub discipline of mathematics. Based upon history, initially, computational physics was the first modern computer application in the area of science and it belong to a subsection of computational science. The computational physics is frequently considered as a sub discipline of theoretical physics, but some people take into account it a bridge between theoretical physics and experimental physics. An area of study that balances theory and research. While the research or experiments that use computers to measure and record data, this is clearly not a computational method.

    In physical science, a number of theories based upon mathematical models provide very accurate calculation results related to system behavior. Unfortunately, a few problems often lead to solving mathematical models for certain systems to produce helpful calculations that are not achievable. This can happen, e.g., as the solution doesn’t possess either a closed-form representation or is too complex. In problems like this, a numerical approach is necessary. Computational physics is a subject that deals with numerical methods such as this, the approach of the solution is represented by various simple mathematical operations (algorithms) and computers are applied to implement tasks like this ones and calculate the approach solution and the corresponding error value.    

       The problem related to computational physics are commonly very difficult to overcome precisely. This is due to a variety of reasons related to mathematics such as: absence of algebraic and / or analytic solutions, level of intricacy and disorder of problems. For instance, the calculation of the wave function of an electron that surrounds on ​​an atom that has a great electric field, will need a great amount of effort to discover a practical algorithm (when we able to find the algorithm). Otherwise, we need a simpler technique such as: the graphical method and the root finding method. For more complicated cases, it often requires perturbation theory. In addition, for several cases in microscopic systems consisting of many particles (many-body problems) with the size of each particle in order 1023 sometimes also becomes a problem. Likewise, solutions related to quantum mechanical problems are usually the size of the system with an exponential order and for the classic case in the N-body is the square of N. So many cases of physics are non-linear in nature, which means it is very difficult to guarantee that errors will not increase large so as to produce a solution that is not suitable with the expected one.

       We can look for computational branches that is suitable to the major fields of physics. Computational fluid dynamics (CFD), computational solid mechanics and computational contact mechanics are few examples related to computational mechanics. In addition, the computational method corresponds to the solid state physics is a very important part that is directly related to materials science. Computational statistical physics uses many methods such as Monte Carlo. This technique is also related to sciences related to social matter, theory of network, mathematical models  both for disease transmission and the spread of forest fires. Computational method that are concern with particle physics commonly associated with some difficulties driven by particle physics. Computational astrophysics constitute the usage of computation to problems related to astrophysical phenomena. Whereas computational biophysics represent a subsection of computational biology and biophysics dealing with a complex and large biological problems.  

       Some methods or algorithms that are usually used in computational physics depend on the mathematical problem to be solved or for what cases the method is applied. For the root search case, we usually use the Newton-Rapshon method. Completion of linear equation systems generally uses methods such as: Gauss elimination, Gauss-Jordan elimination, Gauss-Seidal iteration, lower-upper decomposition (LU decomposition) and others. To solve the case of ordinary differential equations (ODE) the methods used are: Euler and Runge-Kutta. Cases related to partial differential equations (PDE) can be used methods including: finite difference and relaxation. And for the case of the eigen value matrix generally used the Jacobi eigen value algorithm and power iteration. All of the methods mentioned above are employed for calculating the physical natures of the system being modeled. Computational physics also utilizes some ideas that is implemented in computational chemistry, e.g., the density functional theory employed by physicists concerning with solid state research to estimate the properties of solids is essentially similar to that used by chemists for estimation of properties molecular properties. In addition to computational physics includes improving the quality of software and hardware to solve these problems. Because these problems require high processing power and large memory capacity.

       Because of the problems related to computational physics are so extensive that make it a key component of modern investigation in various fields of physics, i.e.: fluid mechanics, plasma physics, physics system simulations (e.g. molecular dynamics), modeling of nuclear engineering, prediction of protein structure, weather forecasting, stock prediction solid physics astrophysics  and so on.